Classification of subgroups of symmetric group S4
Mathematics ·This article tries to identify the subgroups of symmetric group S4 using theorems from undergraduate algebra courses.
Basic Fact
Below we will use the cycle notation to denote subgroup elements.
\(S_4\) has \(4!\) elements. Categorize them by cycle patterns, and we get,
\(\begin{array}
{c|c|c}
Cycle \ Pattern & No. \ of \ elements & Order \\
\hline
(1,): id. & 1 \ elem & (ord(e)=1) \\
(2,1,1):(1,2),(1,3)... & 6 & (ord(\alpha)=2) \\
(3,1): (1,2,3),(1,3,2)... & 8 & (ord(\beta)=3) \\
(2,2): (1,2)(3,4)... & 3 & (ord(\gamma)=2) \\
(4): (1,2,3,4)... & 6 & (ord(\delta)=4) \\
\end{array}\)
Classification
From Lagrange’s Theorem, nontrivial proper subgroups of \(S_4\) should be of order p \(\mid\) 24 for some integer \(p\), i.e., \(p = 2,3,4,6,8\) or 12.
1.Subgroups of order 2
\(H \cong \mathbb{Z_2}\), which is equivalent to \(H = <\sigma>\) for some \(\sigma\), where ord(\(\sigma\))=2. Thus \(S_4\) has 9 subgroups:\(\lbrace <\alpha> \rbrace \cup \lbrace <\gamma> \rbrace\).
2.Subgroups of order 3
\(H \cong \mathbb{Z_3}\), which is equivalent to \(H = <\sigma>\) for some \(\sigma\), where ord(\(\sigma\))=3. Thus \(S_4\) has 8 subgroups:\(\lbrace <\beta> \rbrace\).
3.Subgroups of order 4
The class equation (or just simple reasoning) tells us that any subgroup \(H\) of order 4 is abelian, and thus the fundamental theorem of finite abelian groups tells us \(H \cong \mathbb{Z_4}\) or \(H \cong \mathbb{Z_2} \times \mathbb{Z_2}\). Next we try to find all subgroups by enumerating all cases.
Case 1: \(H \cong \mathbb{Z_4}\)
From cycle patterns, we know that there are 3 cyclic subgroups. (Note that not 6 subgroups: \(<1,2,3,4> = <1,4,3,2>\) and so on.)
Case 2: \(H \cong \mathbb{Z_2} \times \mathbb{Z_2}\)
Denote \(H= \lbrace id,a,b,c \rbrace\), then \(ord(a)=ord(b)=ord(c)=2\), and \(a*b=c,a*c=b,b*c=a\).
Consider the conjugacy class \(\lbrace \alpha \rbrace\) and \(\lbrace \gamma \rbrace\):
1. \(H\backslash \lbrace e \rbrace \subset \lbrace \alpha \rbrace\):
None of such subgroup exists.(The set is not closed.)
2. \(H\backslash \lbrace e \rbrace \subset \lbrace \gamma \rbrace\):
\(H^{(2)} = \lbrace e \rbrace \cup \lbrace \gamma \rbrace\), which is a nontrivial proper abelian (thus normal) subgroup of \(S_4\).
3. \(H\backslash \lbrace e \rbrace \not\subset \lbrace \alpha \rbrace\) and \(H\backslash \lbrace e \rbrace \not\subset \lbrace \gamma \rbrace\):
There are three subgroups, where one element is from {\(\gamma\)} and the other two nontrivial elements are from {\(\alpha\)} correponding to the two adjacent transposition from the element. For example, \(\lbrace id,(1,2)(3,4),(1,2),(3,4) \rbrace\).
4.Subgroups of order 6
\(2=p \mid 2=3-1=q-1\), thus we cannot claim using corollary to Sylow’s Theorem that the subgroup is abelian. However, as no element of \(S_4\) is of order 6, thus \(S_4\) has no abelian subgroup of order 6 by FTFAP.
Using brute force approach or semidirect product \(H\) of order 2 and a normal subgroup \(N\) of order 3, we may claim that \(H=S_3\) up to isomorphism. Thus \(S_4\) has four subgroups of order 6.
5.Subgroups of order 8
Subgroups of order 8 are 2-Sylow subgroups of \(S_4\). Sylow’s third theorem tells us there are 1 or 3 2-Sylow subgroups. Case \(r=1\) can be ruled out, otherwise \(H\) is a normal subgroup in \(S_4\), but there is no such union(group) of conjugacy classes whose cardinality is 8. Thus \(r=3\).
H is not normal in \(S_4\), thus H is not abelian. Lemma to Sylow’s First Theorem gives us that center of H, Z, satisfies \(Z \cong \mathbb{Z_2}\) and \(G/Z \cong \mathbb{Z_2} \times \mathbb{Z_2}\). Refer back to subgroups of order 4(Section 3.2), we may simply use composition of \(H^{(2)}\) and \(\alpha\) to get the three subgroups, e.g., \(\lbrace H^{(2)}, (1,2) H^{(2)}\rbrace\).
6.Subgroups of order 12
\([G:H]=2\), thus \(H^{(1)}\) is a normal subgroup in \(S_4\). Check the cardinality of conjugacy classes, we can get, there exists only one subgroup of order 12, i.e., \(\lbrace e \rbrace \cup \lbrace \beta \rbrace \cup \lbrace \gamma \rbrace\).
In fact, \(H^{(1)} \cong A_4\) the alternating subgroup: elements of \(H^{(1)}\) are even permutations.
Discussion
1. \(S_4\) is a solvable group.
Generate the commutator subgroup sequence, and we can get, \(S_4 = H^{(0)} \supset H^{(1)} \subset H^{(2)} \supset H^{(3)} = \lbrace e \rbrace\).
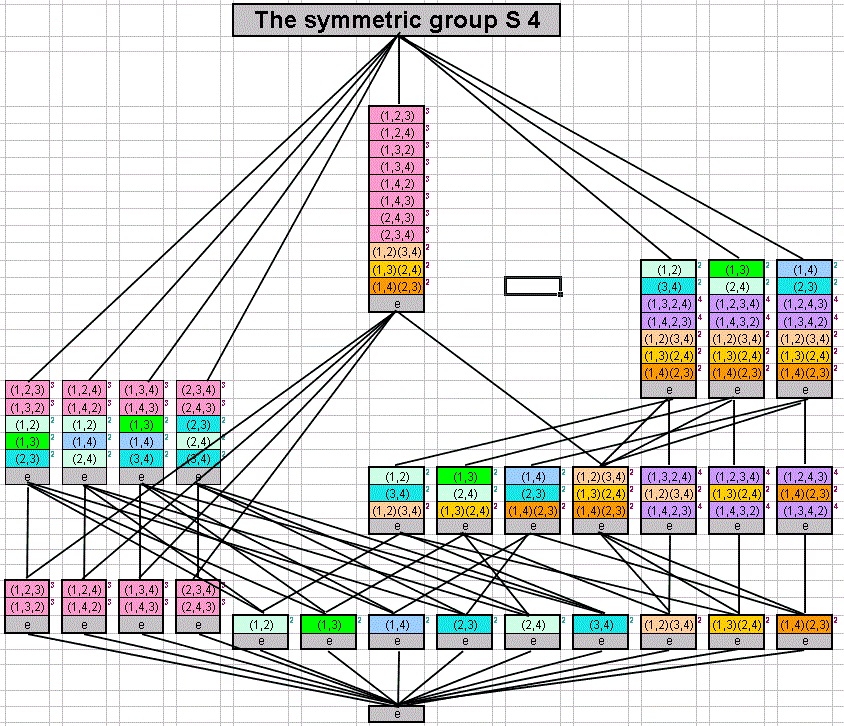
2. Subgroup lattice of \(S_4\)